What Are the Different Systems of Equations? Let's Break It Down!
What Is a System of Equations?
You’ve probably heard the term "system of equations" a lot, especially if you've ever struggled with algebra. I know, I know, it sounds intimidating, right? But once you get the hang of it, it’s actually pretty straightforward. A system of equations is just a set of two or more equations that you solve at the same time. The key idea? You’re looking for values of variables that make all the equations true at once. It's like solving a puzzle, and trust me, the satisfaction of finding that right answer feels awesome.
I remember the first time I tackled a system of equations in high school. At first, I felt totally lost. But after practicing a bit, I got the hang of it—and wow, it clicked! The "aha" moment is real, folks.
Types of Systems of Equations
1. Consistent and Inconsistent Systems
Okay, let’s get into the first big distinction: whether the system is consistent or inconsistent.
Consistent systems have at least one solution. In other words, these equations "agree" with each other, and there’s a point (or multiple points) where their graphs intersect.
Inconsistent systems, on the other hand, have no solution. The equations contradict each other, so their graphs never cross. It’s like trying to find a spot where two lines can meet, but they just won’t. Frustrating, right?
One time, I worked on a system in my college math class that seemed to be inconsistent, but after some digging, I realized that one of my equations was off. That "Aha!" moment came when I fixed it—turns out, it was consistent all along! Don't you love those moments of discovery?
2. Dependent and Independent Systems
Next up: dependent and independent systems. This is where it gets really interesting.
Independent systems have exactly one solution. They are the clean, straightforward ones. You’re just finding the point where the lines intersect. Simple, right?
Dependent systems, however, have infinitely many solutions. What does this mean? Well, the equations actually represent the same line (or surface in more complex cases). So, every point on the line is a solution. I once ran into a dependent system when trying to solve a real-world problem in economics, and I found that the two equations were basically different ways of describing the same thing. Mind-blowing!
3. Homogeneous vs Non-Homogeneous Systems
Let’s add another layer of complexity with homogeneous and non-homogeneous systems.
Homogeneous systems are those where all the constant terms are zero. The equations always have at least one solution—the trivial one, where all variables equal zero. It's like the "default" solution.
Non-homogeneous systems are the ones where the constants aren’t zero. These can have no solution, one solution, or many solutions, depending on how the equations line up.
I’ll never forget a time when I was solving a homogeneous system and thought it was impossible. But when I realized the trivial solution (everything equals zero) was still valid, it felt like I was cheating the system—like discovering the cheat code for life!
Methods for Solving Systems of Equations
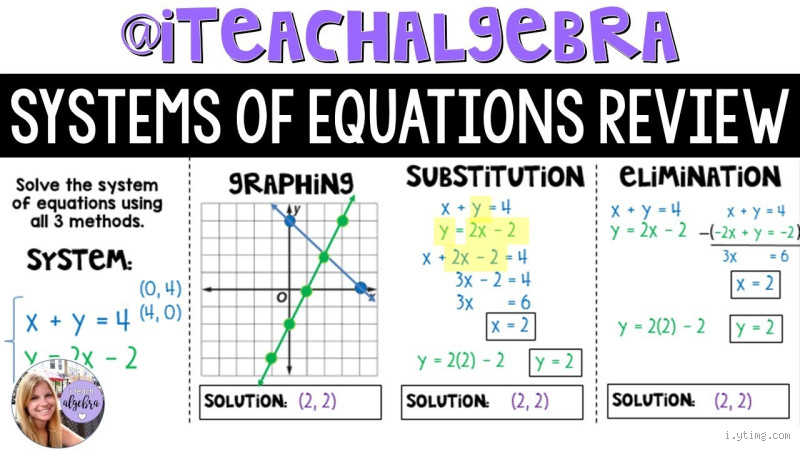
1. Graphing Method
Graphing is the most intuitive method, but let’s be real—it’s not always the most efficient, especially if the equations are complicated.
You graph each equation on the same coordinate plane, and the solution is the point where the lines (or curves) intersect. If the lines don’t meet, it’s inconsistent. If they overlap completely, it’s dependent. This method can be fun if you're visual but can get messy quickly if the numbers are big or the equations are complex. I’ve definitely made that mistake before—spending way too much time plotting, only to realize I could’ve used a quicker method.
2. Substitution Method
Substitution is a personal favorite of mine. You solve one of the equations for one variable and substitute that expression into the other equation(s). It’s like replacing one unknown with a known value and simplifying from there.
I remember the first time I used substitution on a system of two equations. It felt like magic when I saw the equations collapse down to one. It was so much cleaner than graphing, and the satisfaction was real.
3. Elimination Method
This method involves adding or subtracting equations to eliminate one of the variables. It’s powerful and effective, especially when you’re dealing with more complex systems.
One time, I was working through an elimination problem that had me stumped. I kept making the same mistake and couldn’t get rid of a variable. But after a few tries, I figured out that I needed to multiply one of the equations by a factor to make the coefficients match. Once I did that, boom—the variables cancelled out, and I could solve it!
4. Matrix Method
Okay, I know, matrices sound a bit intimidating. But trust me, once you get used to them, they’re a game-changer, especially for larger systems. The matrix method uses something called augmented matrices to solve systems of linear equations. It’s super efficient when you have systems with three or more variables. If you're dealing with a system in a real-world context (like economics or engineering), this method is often the go-to for efficiency.
Why Understanding Systems of Equations Matters
Systems of equations show up everywhere. Whether you’re solving a problem about cost and revenue, planning a trip with multiple variables, or figuring out the most efficient way to allocate resources in business, understanding how to solve these systems can help you make better decisions.
It’s funny—I used to think this stuff was just for classroom problems, but then I started applying it in real-life situations. I recently helped a friend set up a budget using a system of equations, and the method worked perfectly to balance income with expenses. It was one of those "I can’t believe I’m using this stuff in real life!" moments.
In the end, there are several systems of equations, each with its own characteristics and methods for solving them. Whether you're dealing with consistent or inconsistent systems, or whether you’re using graphing, substitution, or elimination, the most important thing is to practice and find the method that works best for you. So, next time you tackle a system, remember—it’s just a puzzle waiting for you to solve.
How much height should a boy have to look attractive?
Well, fellas, worry no more, because a new study has revealed 5ft 8in is the ideal height for a man. Dating app Badoo has revealed the most right-swiped heights based on their users aged 18 to 30.
Is 172 cm good for a man?
Yes it is. Average height of male in India is 166.3 cm (i.e. 5 ft 5.5 inches) while for female it is 152.6 cm (i.e. 5 ft) approximately. So, as far as your question is concerned, aforesaid height is above average in both cases.
Is 165 cm normal for a 15 year old?
The predicted height for a female, based on your parents heights, is 155 to 165cm. Most 15 year old girls are nearly done growing. I was too. It's a very normal height for a girl.
Is 160 cm too tall for a 12 year old?
How Tall Should a 12 Year Old Be? We can only speak to national average heights here in North America, whereby, a 12 year old girl would be between 137 cm to 162 cm tall (4-1/2 to 5-1/3 feet). A 12 year old boy should be between 137 cm to 160 cm tall (4-1/2 to 5-1/4 feet).
How tall is a average 15 year old?
Average Height to Weight for Teenage Boys - 13 to 20 Years
| Male Teens: 13 - 20 Years) | ||
|---|---|---|
| 14 Years | 112.0 lb. (50.8 kg) | 64.5" (163.8 cm) |
| 15 Years | 123.5 lb. (56.02 kg) | 67.0" (170.1 cm) |
| 16 Years | 134.0 lb. (60.78 kg) | 68.3" (173.4 cm) |
| 17 Years | 142.0 lb. (64.41 kg) | 69.0" (175.2 cm) |
How to get taller at 18?
Staying physically active is even more essential from childhood to grow and improve overall health. But taking it up even in adulthood can help you add a few inches to your height. Strength-building exercises, yoga, jumping rope, and biking all can help to increase your flexibility and grow a few inches taller.
Is 5.7 a good height for a 15 year old boy?
Generally speaking, the average height for 15 year olds girls is 62.9 inches (or 159.7 cm). On the other hand, teen boys at the age of 15 have a much higher average height, which is 67.0 inches (or 170.1 cm).
Can you grow between 16 and 18?
Most girls stop growing taller by age 14 or 15. However, after their early teenage growth spurt, boys continue gaining height at a gradual pace until around 18. Note that some kids will stop growing earlier and others may keep growing a year or two more.
Can you grow 1 cm after 17?
Even with a healthy diet, most people's height won't increase after age 18 to 20. The graph below shows the rate of growth from birth to age 20. As you can see, the growth lines fall to zero between ages 18 and 20 ( 7 , 8 ). The reason why your height stops increasing is your bones, specifically your growth plates.
